Gödel’s completeness theorem: Difference between revisions

On Apr 19, 2023

Line 4: Line 4:

”’Gödel’s completeness theorem”’ is a fundamental theorem in [[mathematical logic]] that establishes a correspondence between [[semantics|semantic]] truth and syntactic [[Provability logic|provability]] in [[first-order logic]].

The completeness theorem applies to any first-order [[Theory (mathematical logic)|theory]]: If ”T” is such a theory, and φ is a sentence (in the same language) and every model of ”T” is a model of φ, then there is a (first-order) proof of φ using the statements of ”T” as axioms. One sometimes says this as “anything universally true is provable”. This does not contradict [[Gödel’s incompleteness theorem]], which shows that some formula φ_u is unprovable although true in the natural numbers, which are a particular model of a first-order theory describing them — φ_u is just false in some other model of the first-order theory being considered (such as a [[non-standard model of arithmetic]] for [[Peano arithmetic]]). This kind of failure of consistency between a standard and non-standard model is also called Omega Inconsistency. {{Cite arXiv|last=Batzoglou|first=Serafim|eprint=2112.06641|title=Gödel’s Incompleteness Theorem|year=2021}} (p.17). Accessed 2022-12-01.

The completeness theorem applies to any first-order [[Theory (mathematical logic)|theory]]: If ”T” is such a theory, and φ is a sentence (in the same language) and every model of ”T” is a model of φ, then there is a (first-order) proof of φ using the statements of ”T” as axioms. One sometimes says this as “anything universally true is provable”. This does not contradict [[Gödel’s incompleteness theorem]], which shows that some formula φ_u is unprovable although true in the natural numbers, which are a particular model of a first-order theory describing them — φ_u is just false in some other model of the first-order theory being considered (such as a [[non-standard model of arithmetic]] for [[Peano arithmetic]]). This kind of failure of consistency between a standard and non-standard model is also called Omega Inconsistency.{{Cite arXiv|last=Batzoglou|first=Serafim|eprint=2112.06641|title=Gödel’s Incompleteness Theorem|year=2021}} (p.17). Accessed 2022-12-01.

It makes a close link between [[model theory]] that deals with what is true in different models, and [[proof theory]] that studies what can be formally proven in particular [[formal system]]s.

Fundamental theorem in mathematical logic

The formula (∀x. R(x,x)) → (∀x∃y. R(x,y)) holds in all structures (only the simplest 8 are shown left). By Gödel’s completeness result, it must hence have a natural deduction proof (shown right).

Gödel’s completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic.

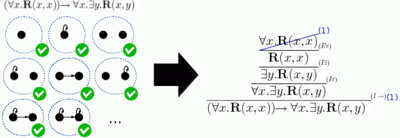
The completeness theorem applies to any first-order theory: If T is such a theory, and φ is a sentence (in the same language) and every model of T is a model of φ, then there is a (first-order) proof of φ using the statements of T as axioms. One sometimes says this as “anything universally true is provable”. This does not contradict Gödel’s incompleteness theorem, which shows that some formula φ_u is unprovable although true in the natural numbers, which are a particular model of a first-order theory describing them — φ_u is just false in some other model of the first-order theory being considered (such as a non-standard model of arithmetic for Peano arithmetic). This kind of failure of consistency between a standard and non-standard model is also called Omega Inconsistency.^[1]

It makes a close link between model theory that deals with what is true in different models, and proof theory that studies what can be formally proven in particular formal systems.

It was first proved by Kurt Gödel in 1929. It was then simplified when Leon Henkin observed in his Ph.D. thesis that the hard part of the proof can be presented as the Model Existence Theorem (published in 1949).^[2] Henkin’s proof was simplified by Gisbert Hasenjaeger in 1953.^[3]

Preliminaries[edit]

There are numerous deductive systems for first-order logic, including systems of natural deduction and Hilbert-style systems. Common to all deductive systems is the notion of a formal deduction. This is a sequence (or, in some cases, a finite tree) of formulae with a specially designated conclusion. The definition of…